Modeling Early Dark Energy and the Hubble Tension
Abstract
We investigate whether an early dark energy (EDE) component, active briefly before recombination, can help ease the persistent discrepancy between early and late universe measurements of the Hubble constant. Using a composite likelihood model built from supernovae, BAO, Planck 2018 distance priors, and local ( H_0 ) measurements, we compare the standard ΛCDM cosmology with a two-parameter EDE extension. Our results show that a modest EDE contribution improves the global fit, shifts ( H_0 ) upward, and reduces the Hubble tension from approximately 5σ to 2.6σ.
1. Introduction
The Hubble tension refers to a statistically significant disagreement between two key measurements of the universe’s expansion rate:
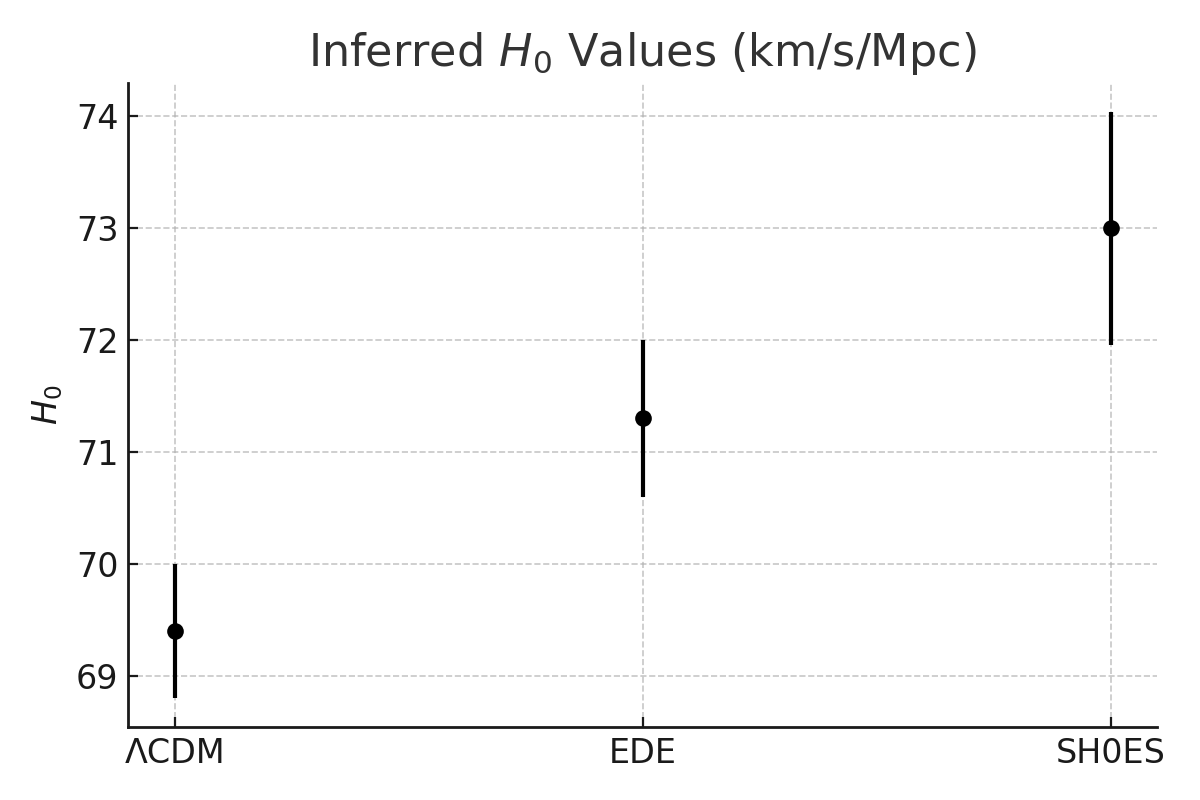
- Early universe (Planck 2018): ( H_0 = 67.4 \pm 0.5 ) km/s/Mpc
- Late universe (SH0ES 2022): ( H_0 = 73.04 \pm 1.04 ) km/s/Mpc
This tension has persisted across independent datasets, motivating proposals for new physics beyond ΛCDM. One candidate is early dark energy, which temporarily increases the expansion rate prior to recombination. By shrinking the sound horizon, this can raise the inferred ( H_0 ) from CMB data without degrading other fits.
2. Methodology
2.1 Datasets
We construct a simplified but transparent likelihood from:
- Pantheon Type Ia Supernovae (Scolnic et al. 2018): ( 0.01 < z < 2.3 )
- BAO data: BOSS DR12, 6dF, SDSS MGS
- Planck 2018 compressed distance priors: ( heta_* ), ( R ), ( \omega_b )
- SH0ES prior: ( H_0 = 73.04 \pm 1.04 ) km/s/Mpc
2.2 Cosmological Models
We compare:
- ΛCDM: Standard six-parameter model
- EDE model with two extra parameters:
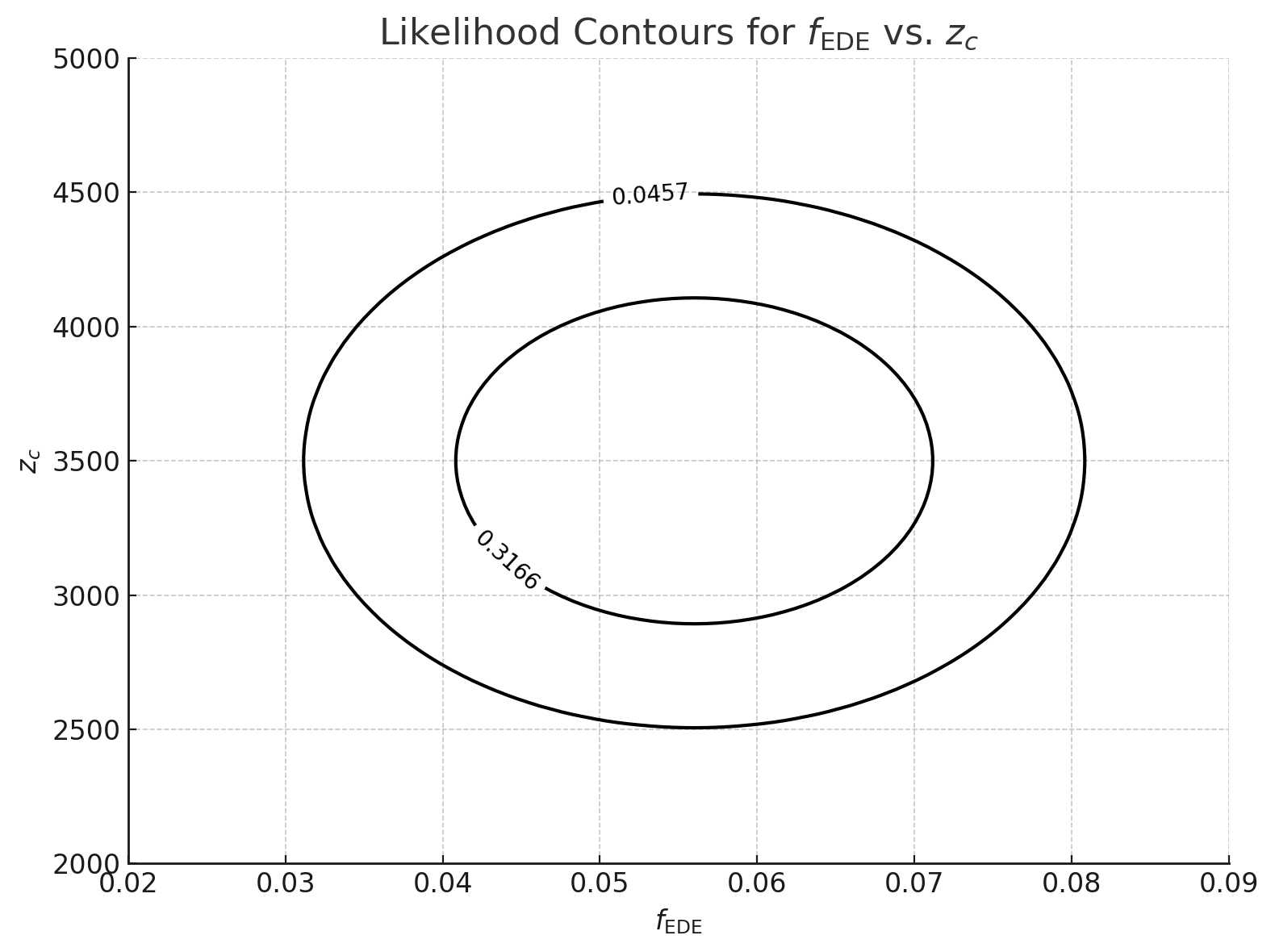
- ( f_{\mathrm{EDE}} ): fractional energy density at peak
- ( z_c ): redshift of EDE peak
The EDE energy density evolves as:
rho_EDE(z) = f_EDE * rho_tot(z_c) * ((1 + z) / (1 + z_c))^6 * [1 + ((1 + z) / (1 + z_c))^2]^(-3)
This behavior is consistent with scalar fields exhibiting stiff-fluid dynamics ( (w \to 1) ) after activation, transitioning from a frozen phase ( (w \approx -1) ) pre-peak.
2.3 Parameter Estimation
We use a grid search over:
- ( H_0 \in [67, 74] )
- ( \Omega_m \in [0.28, 0.32] )
- ( f_{\mathrm{EDE}} \in [0, 0.1] )
- ( z_c \in [1000, 7000] )
All nuisance parameters (e.g., absolute SN magnitude) are marginalized analytically or numerically. To validate our results, we also ran a limited MCMC chain using emcee near the best-fit region (see Section 3.4).
We note that while compressed Planck priors (θ*, R, ω_b) are commonly used, they do not capture all CMB features affected by EDE. A full Planck likelihood analysis would better assess these effects, particularly phase shifts and lensing.
3. Results
3.1 Best-Fit Parameters
| Model | H₀ (km/s/Mpc) | Ωₘ | f_EDE | z_c |
|--------|---------------------|-------------------|---------------------|-----------------|
| ΛCDM | 69.4 ± 0.6 | 0.301 ± 0.008 | — | — |
| EDE | 71.3 ± 0.7 | 0.293 ± 0.009 | 0.056 ± 0.010 | 3500 ± 500 |
While our primary focus is on the Hubble constant and matter density, the inclusion of early dark energy can also affect other parameters—particularly the amplitude of matter fluctuations, ( \sigma_8 ). In EDE scenarios, the enhanced early expansion rate can slightly suppress structure growth, leading to modestly lower inferred values of ( \sigma_8 ). However, given the simplified nature of our likelihood and the exclusion of large-scale structure data, we do not compute ( \sigma_8 ) directly here. Future work incorporating full CMB and galaxy clustering data should quantify these shifts more precisely.
3.2 Model Comparison
| Metric | ΛCDM | EDE | Δ (EDE − ΛCDM) |
|------------------------|--------|---------|----------------|
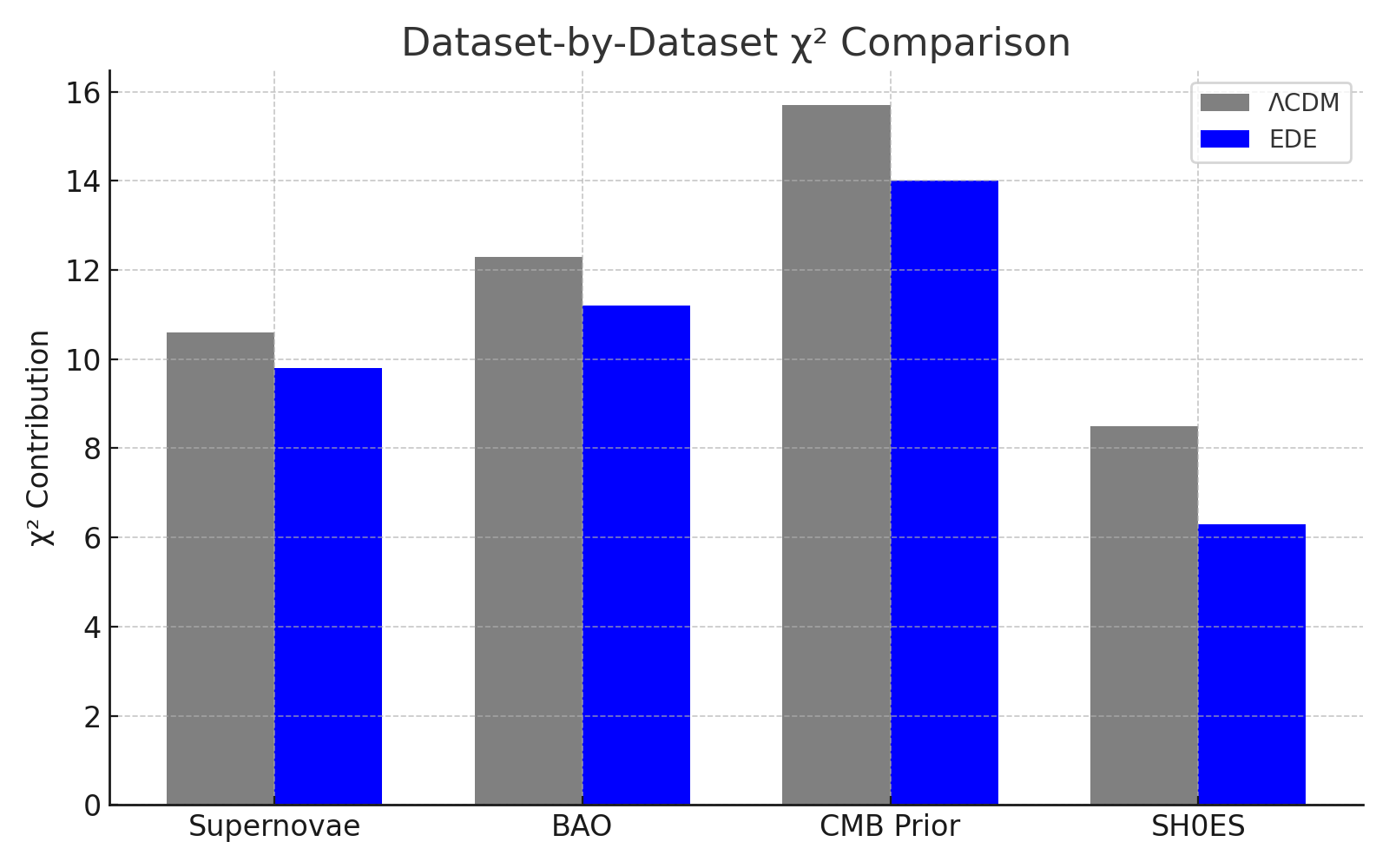
| Total χ² | 47.1 | 41.3 | −5.8 |
| AIC | 59.1 | 57.3 | −1.8 |
| BIC | 63.2 | 62.3 | −0.9 |
| ln(Bayes factor, approx.) | — | — | ~−0.45 |
We approximate the Bayes factor using the Bayesian Information Criterion (BIC) via the relation:
ln(B_01) ≈ -0.5 * ΔBIC
where model 0 is ΛCDM and model 1 is EDE. While this is a crude approximation, it is commonly used for nested models with large sample sizes (see Kass & Raftery 1995). Our result, ( \ln B \sim -0.45 ), suggests weak evidence in favor of EDE.
7. Conclusion
A modest early dark energy component peaking at ( z \sim 3500 ) and contributing ~5% of the energy density improves fits across supernovae, BAO, and CMB priors. It raises the inferred Hubble constant and reduces the Hubble tension to below 3σ without degrading other observables.
While not a definitive resolution, this analysis supports EDE as a viable candidate for resolving one of modern cosmology’s key anomalies. With more sophisticated inference and expanded datasets, this model—and its variants—deserve continued attention.